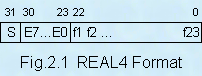
where:
S = sign bit (0=positive, 1=negative)
En = biased exponent bits
fn = fraction bits of the significand
(Reminder: Addressing mode syntax in this document is that of the MASM assembler. The syntax may vary with other assemblers/compilers for the described addressing modes and should be modified as required.)
There are three general data types which can be used by the FPU: integer, floating point and packed BCD.
In the context of FPU operations, integers are whole numbers, i.e. numbers which do not contain any fractional part. All integers used in FPU instructions are also considered as signed integers, the most significant bit being 0 for positive values or 1 for negative values.
Negative integer values are represented by taking the 2's complement of the positive value and adding 1 (2's complements are obtained simply by inverting each bit of the number). As a refresher, the following example would be for a decimal value of 6235 in a 16-bit WORD.
0001 1000 0101 1011 185Bh +6235d
1110 0111 1010 0100 2's complement
+ 1
-------------------
1110 0111 1010 0101 E7A5h -6235d
Within the integer data types, three sizes of integers may be used: the 16-bit WORD, the 32-bit DWORD, and the 64-bit QWORD, (the 8-bit byte cannot be used with FPU instructions). The available range of values for each of those sizes is as follows:
WORD range ±(215-1) or ±32767 DWORD range ±(231-1) or ±2147483647 QWORD range ±(263-1) or ±9223372036854775807
Addressing modes of integer numbers
All integer data used with FPU instructions can only be accessed through memory locations. The actual code generated by the assembler is different for each of the allowed integer sizes.
Integer values in memory can be specified by any of the acceptable addressing modes. For example, if a memory variable (global or local) has been declared as a WORD, the variable's name (whether it is indexed or not) is sufficient to get it treated as the declared size. However, if CPU registers are used as pointers to data in memory, it is imperative that the index be qualified as pointing to the appropriate size. Examples of referring to memory data are:
var_name ;the value of var_name being treated according to how that variable had been declared as a WORD, DWORD or QWORD
var_name[24] ;value starting at the 24th byte of the var_name variable according to how it had been declared
var_name[ebx] ;value starting at the EBX displacement in bytes of the var_name variable according to the above
word ptr [eax] ;informs the processor that EAX points to a 16-bit value
dword ptr [esi+12] ;ESI points to an array of 32-bit values
qword ptr [edi+ebx] ;EDI or EBX points to an array of 64-bit values
dword ptr [ebp+8] ;typical coding for pushed parameters of procedures when coded by the assembler
The CPU registers cannot be used directly as the source or destination of integer data related to the FPU (as opposed to using them as pointers to the location of data in memory). If the need should arise to use the actual value in one of the CPU registers as the operand for data in an FPU instruction, the following is suggested (the 16-bit signed value in AX being used for this example):
push ax ;copies the value in AX to the stack or
;prepares the stack for storing a value
fixxx word ptr [esp] ;fixxx being one of the FPU instructions
;operating on integer data
pop ax ;restores the stack or
;retrieves in AX the integer value stored by the FPU
For numerous reasons, the popped CPU register in the above example could be different from the one which was pushed. Several other CPU and/or FPU instructions could also be inserted between the push/pop instructions. And, an FWAIT instruction may need to precede the pop instruction if its purpose is to retrieve a value stored by the FPU.
Code similar to the above could be used for DWORD values in 32-bit registers.
For QWORD values, such as obtained from a signed multiplication with the result in the EDX/EAX register pair, the sequence would need to be:
push edx
push eax
fild qword ptr [esp]
pop eax
pop edx
The floating point data types are simply binary numbers represented in a manner similar to the scientific notation used for decimal values. For example:
211 = 2.11 x 102 (2.11E+0002)
(The latter is the conventional syntax for decimal values in scientific notation when superscripts are not allowed in a text. For instance, most assemblers/compilers would not recognize superscripts.)
If the above is divided by a multiple of 10 such as 100000, the only thing which would change in the scientific notation would be the exponent:
211 ÷ 100000 = 0.00211 = 2.11 x 10-3 (2.11E-0003)
In binary, the 211 value could be expressed as:
11010011 = 1.1010011 x 27
In this case, if the above is divided by a multiple of 2 (such as 8), again the only thing which would change in the "binary scientific notation" would be the exponent:
11010011 ÷ 23 = 1.1010011 x 24
As can be deduced, this allows for the representation of binary fractions, and of very large or very small values. The formatting of this "binary scientific notation" was standardized for the original CPUs and is usually called the IEEE (Institute of Electrical and Electronics Engineers) real number format.
This real number format consists basically in dividing a binary numerical data into three fields: a sign field, an exponent field, and a number description (significand) field. The exponent field is biased to the middle of the available range such that negative exponents are effectively smaller than positive exponents. And, as opposed to the negative integer system of 2's complements, the significand field is always that of the positive number, negative numbers being distinguished strictly by the sign field.
Within the floating point data types, three sizes of real numbers are available:
the 32-bit REAL4 (also called short real or single precision),
the 64-bit REAL8 (also called long real or double precision),
the 80-bit REAL10 (also called temporary real or extended precision).
The REAL4 floating point number has the following format.
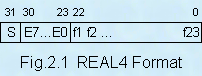
where:
S = sign bit (0=positive, 1=negative)
En = biased exponent bits
fn = fraction bits of the significand
For REAL4 numbers, the bias of the 8 exponent's bits is 7Fh (the last 7 bits). This means that if the real exponent is 0, the value of the exponent field would be 7Fh. When the exponent is negative (i.e. for absolute values lower than 1), the value in the exponent field would be lower than 7Fh, and vice versa for values of 2 and higher.
The maximum value of FFh in the exponent field is reserved for a special category of numbers designated as NAN (Not-A-Number). This category includes the special value of INFINITY and will be described later in more details.
The value of 0 in the exponent field is also reserved for a special category of numbers. When all bits in the significand field are also 0, the value of the REAL number would be equal to 0. If any of the bits in the significand field are set, the value is then called a "denormalized" REAL number. This will also be described later in more details.
Because a valid number in real format must always start with a 1, that first bit is implied in the REAL4 format and the significand field only contains the fraction bits f1, f2, etc. A value of +1.0 would thus be represented in REAL4 format as:
0 01111111 00000000000000000000000b (or 3F800000h in hex notation)(Spaces are left in the binary representation to delineate the 3 fields.
The value of +2.0 (1.0 x 21) would be:
0 10000000 00000000000000000000000b (or 40000000h in hex notation) S 7Fh+1 fraction bits
And the value of -2.0 would be:
1 10000000 00000000000000000000000b (or C0000000h in hex notation)
The result of dividing -211 by 8 would give -1.1010011 x 24 in binary scientific format and its REAL4 representation would be:
1 10000011 10100110000000000000000 (or C1D30000h in hex notation)S 7Fh+4 fraction bits
As with all other numerical data, all REAL numbers are stored in memory with the least significant bytes first. The value of +1.0 in REAL4 format would thus appear in consecutive bytes of memory as:
00 00 80 3F
The largest number which can be represented properly within the REAL4 format is when the exponent field contains FEh and the significand is almost equal to 2 (or almost 280h =2128d or approx. 3.40x1038). The smallest one would be when the exponent field contains 1 and the significand contains all 0s (or 2-7Eh =2-126d or approx. 1.17x10-38).
The 24 bits describing the number (23 bits in the significand field + 1 implied bit) is approximately equivalent to 7 decimal digits.
The REAL8 floating point number has the following format.
For REAL8 numbers, the bias of the 11 exponent's bits is 3FFh (the last 10 bits). The maximum value of 7FFh in the exponent field is reserved for NANs, and the value of 0 in that field has the same purpose as described for the REAL4 format.
As with the REAL4 format, the first bit of the number is implied and the significand field only contains the fraction bits f1, f2, etc. A value of +1.0 would thus be represented in REAL8 format as:
0 01111111111 0000000000000000000000000000000000000000000000000000b (or 3FF0000000000000h in hex notation).
The largest number which can be represented properly within the REAL8 format is when the exponent field contains 7FEh and the significand is almost equal to 2 (or almost 2400h =21024d or approx. 1.79x10308). The smallest one would be when the exponent field contains 1 and the significand contains all 0s (or 2-3FEh =2-1022d or approx. 2.22x10-308).
The 53 bits describing the number (52 bits in the significand field + 1 implied bit) is approximately equivalent to 15 decimal digits.
The REAL10 floating point number has the following format. That is the format used by the FPU's 80-bit data registers. (Real numbers in this format can be stored in memory but must be present in one of the FPU data registers in order to use them with other FPU instructions.)
For REAL10 numbers, the bias of the 15 exponent's bits is 3FFFh (the last 14 bits). The maximum value of 7FFFh in the exponent field is reserved for NANs, and the value of 0 in that field has the same purpose as described for the REAL4 format.
As opposed to the REAL4 and REAL8 formats, the first bit of the number is explicitly included in the significand field and followed by the fraction bits f1, f2, etc. A value of +1.0 would thus be represented in REAL10 format as:
0 011111111111111 10000...........0b (or 3FFF1000000000000000h in hex notation).
The largest number which can be represented properly within the REAL10 format is when the exponent field contains 7FFEh and the significand is almost equal to 2 (or almost 24000h =216384d or approx. 1.19x104932). The smallest one would be when the exponent field contains 1 and the significand's fraction bits contains all 0s (or 2-3FFEh =2-16382d or approx. 3.36x10-4932).
The 64 bits of the significand describing the number is approximately equivalent to 19 decimal digits.
Floating point values in memory can be declared as REA4, REAL8 or REAL10, but can also be declared simply as DWORD, QWORD or TBYTE respectively. When the latter is used and the variable is initialized, it would be assembled as a floating point value if the initializing value is in the scientific decimal format or contains at least one integer digit, a decimal point and at least one decimal digit. (It would be assembled as an integer if no decimal point is present.)
When a floating point memory variable has been declared as one of the above, the variable's name (whether it is indexed or not) is sufficient to get it treated as the declared size. Examples given for declared integer variables would also apply for floating point variables. Although integer variables can also have identical sizes, specific FPU instructions are provided for each data type; there could never be any confusion for the assembler.
Rule #3: The proper instruction must be used with the proper data type
This same rule also applies when using indirect indexing for floating point values. When using CPU registers as pointers to floating point data in memory, it is imperative that the index be qualified as pointing to the appropriate size. Examples of using pointers to floating point data in memory when used with the proper FPU instructions are:
dword ptr [eax] ;informs the processor that EAX points to a REAL4 value
dword ptr [esi+12] ;ESI would point to an array of REAL4 values
qword ptr [edi+ebx] ;EDI or EBX points to an array of REAL8 values
tbyte ptr [edx] ;EDX points to a REAL10 value
dword ptr [ebp+8] ;typical coding for pushed REAL4 parameters of procedures when coded by the assembler
Floating point values in the FPU's data registers can also be accessed with numerous FPU instructions. Since those are always 80-bit values, there is obviously no need to specify their size. As indicated in the previous chapter, their addressing mode is simply:
ST(0), ST(1), ...., ST(7)
Whenever all the bits are set to 1 in the exponent field of a real number format, the value is designated as a NAN. Two values in that category are generated by the FPU: In addition to the exponent field bits being all set to 1, the value of INFINITY has the following special coding to differentiate it from other NANs:
All fraction bits of the significand field are 0 (the explicit 1 in bit 63 remains set for
the REAL10 format). In addition,
Such values of INFINITY are generated by the FPU when
- attempting to divide a valid number by 0 (Zero divide exception detected)
- the result of a computation exceeds the maximum value allowable (Overflow exception
detected)
- instructed to store a value larger than the upper limit of the destination format (Overflow exception detected).
This INFINITY value can be used as an operand in FPU instructions. Depending on the instruction, the result can vary and exceptions may or may not be detected.
In addition to the exponent field bits being all set to 1, the value of INDEFINITE has the following special coding to differentiate it from other NANs:
The 1st fraction bit of the significand field (f1) is set to 1, all other fraction bits being 0 (the explicit 1 in bit 63 remains set for the REAL10 format), and the sign bit is set.
Such a value of INDEFINITE is generated by the FPU whenever a reasonable result is impossible for the given instruction. An Invalid exception is detected in some cases. Examples are:
- using the value of INDEFINITE as an operand
- using an empty register as an operand
- subtracting two values of INFINITY
- extracting the square root of a negative number.
Apart from the INFINITY and INDEFINITE values which can be generated by the FPU, there is a very large number of other NANs with all the possible permutations of fraction bits and sign bit being set to 1 when all the bits in the exponent field are set to 1. For example, the short REAL4 format could have over 16 million of them (224-3 to be more exact).
There are two general categories of other NANs, the QNANs (Quiet NAN) and the SNANs (Signaling NAN). The difference betwen the two is that the first fraction bit is 1 for the QNAN (such as for the special INDEFINITE NAN) and 0 for the SNAN (but with at least one other fraction bit set to 1).
Although NANs could be used as valid operands with some of the FPU instructions, they are of no practical use for the average programmer.
The lowest value of the exponent field in a real number format is 1 if the number is to be considered "normal". Any further reduction of that small number may cause the value in the exponent field to become 0.
Although the exponent field cannot be lower than 0, some numbers smaller than the smallest normal one can still be expressed when the exponent field becomes 0. The FPU does this by shifting the fraction bits to the right (along with the implicit or explicit 1) with some loss of precision due to the loss of the right-most bits. Those numbers are then qualified as denormalized.
This concept should be easier to visualize with an example using a REAL4 small number, the smallest one being 1x2-7Eh for that format.
The result of dividing the previously used decimal value of 211 by 286h would be:
1.1010011 x 27 ÷ 286h = 1.1010011 x 2-7Eh which, in REAL4 format, would still be in the
"normal number" range:
For maximum accuracy, intermediate results of computations should never be stored in the REAL4 or REAL8 formats unless there is absolute certainty that the "normal number" limits of those formats would not be exceeded.
The Packed BCD (Binary Coded Decimal) data type is considered by the FPU as a signed integer and has the following 80-bit special packed decimal format.
For example, the decimal value 211 in this data type format would be:
36 55 06 00 00 00 00 00 00 80
As depicted, 18 decimal digits is the maximum which can be inserted in this format. The largest integer which could be represented in this format would thus be 18 consecutive 9 (or 1018-1). Packed BCD variables in memory can be declared only as TBYTE. Such variable is rarely, if ever, initialized. Its purpose is usually to reserved a memory space to either convert decimal strings into a format which will be acceptable to the FPU, or to instruct the FPU where to store a number after converting it to this format.
Only two FPU instructions can use this data format and are specific for only this format. It is therefore never necessary to specify this memory data size, whether it is addresses by the variable's name or by a pointer. Examples of referring to memory data with the packed BCD FPU instructions are:
var_name ;the variable var_name must have been declared as a TBYTE, otherwise the assembler issues an error
var_name[30] or var_nam[ebx] ;same as above with displacement
[edi] ;this will use the 10 bytes starting at the address pointed to by the register
All other legitimate modes of indirect addressing are also acceptable. When using pointers, the programmer is responsible for insuring that the 10 bytes of memory at that address are suitable for the purpose.
Addressing modes of real numbers
INFINITY and INDEFINITE.
when the sign bit is 0, that NAN is treated as +INFINITY
when the sign bit is 1, that NAN is treated as -INFINITY
0 00000001 10100110000000000000000 (or 00D30000h in hex notation).
Dividing the above by 2 would now yield the following denormalized number:
0 00000000 11010011000000000000000 (or 00698000h in hex notation).
Dividing it again by 2 would give:
0 00000000 01101001100000000000000 (or 0034C000h in hex notation).
By repeating such division, the result would eventually become:
0 00000000 00000000000000000000001 (or 00000001h in hex notation).
It should now have become obvious that denormalized numbers suffer a loss of
precision as they get smaller until they eventually reach a value of zero. Although these denormalized numbers can be used by the FPU with all its instructions, this potential loss of precision must be fully understood by the programmer. Using floating point maths is not by itself a guarantee of accuracy.
where:
S = sign bit (0=positive, 1=negative)
dn = 4-bit decimal values, d0 being the least significant
(bits 72-78 are not used and ignored)
00000000000000000211h in hex notation
The decimal value of -65536 (-216) in this data type format would be:
80000000000000065536h in hex notation
As with all other numerical data, the packed BCD format is stored in memory with the least significant bytes first. The consecutive memory bytes (in hex notation) of the above number would thus be:
Addressing modes of packed BCD numbers
SIMPLY FPU
CONTENTS